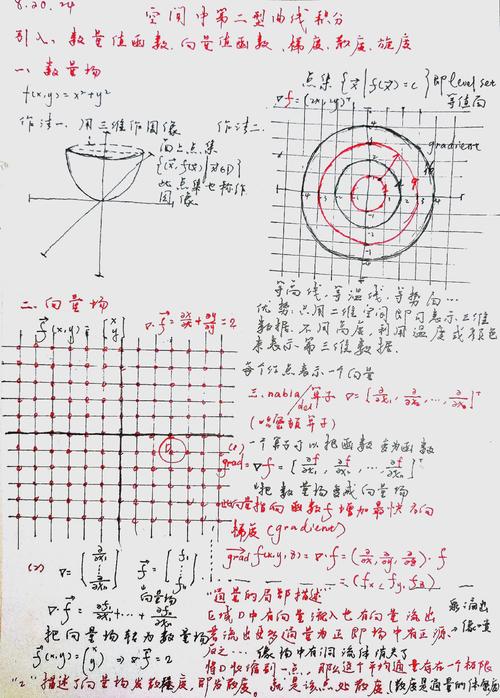
老铁们,近在玩儿一个巨有意思的游戏,名字就叫“斯托克斯公式怎么用”。可不是真的游戏,是高等数学里一个公式,但我觉得它玩儿起来比很多游戏都刺激!这公式看着挺吓人,一堆符号,密密麻麻的,但其实只要掌握了技巧,它比想象中简单得多。我个人觉得,这玩意儿就像个大型解密游戏,你要一步步解开它背后的秘密。
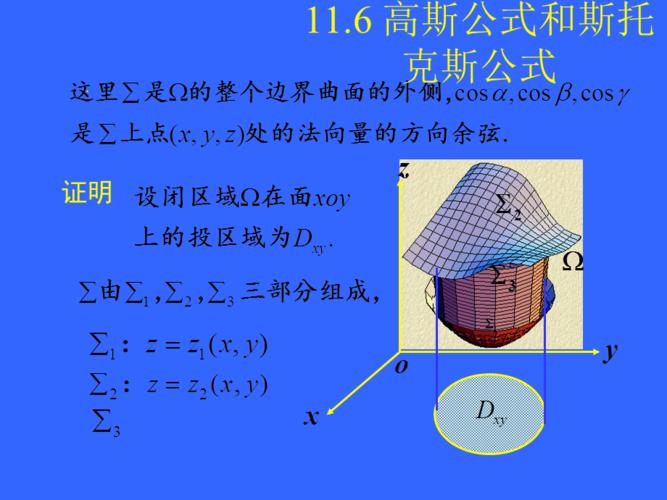
咱们得搞清楚这斯托克斯公式是干啥的。简单来说,它就是连接曲线积分和曲面积分的一个桥梁。想象一下,你手里有两个积分,一个是沿着一条曲线算的,一个是算一个曲面的。这俩看着八竿子打不着,但斯托克斯公式就能把它们联系起来,让你能用其中一个来算另一个。这感觉就像游戏里的两个不同的任务,看似独立,其实背后暗藏玄机,你找到了连接点,就能事半功倍。
这公式具体咋用呢?别慌,咱们一步一步来。你要确认你的积分是不是符合斯托克斯公式的条件。这就像游戏里,你要先看自己是不是满足任务的条件,才能开始游戏。条件很简单,你的曲线必须是闭合的,也就是首尾相连的;你的曲面必须是以这条曲线为边界的。如果条件不满足,那可就玩儿不下去了。
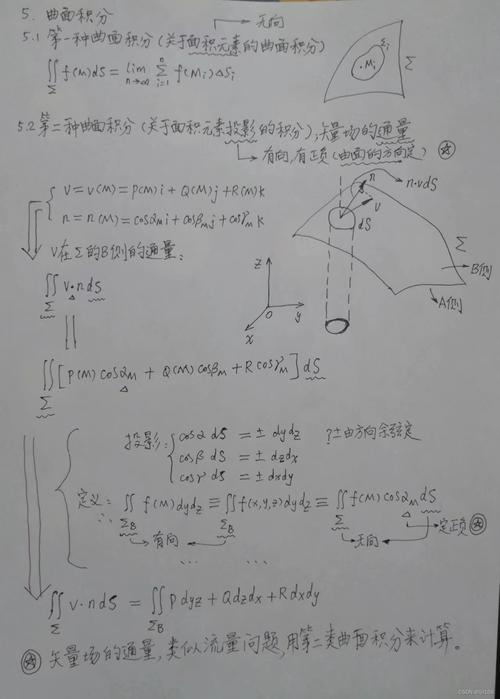
满足条件之后,咱们就可以开始“游戏”了。你需要算出你的曲面的旋度。这旋度,你可以把它想象成曲面上每个点的“旋转速度”。这步运算有点复杂,但别怕,多练练就好。这就像游戏里的技能学习,一开始可能有点难,但熟能生巧。
然后,你需要对这个旋度进行曲面积分。这就像游戏里,你要收集各种资源,完成任务目标。这个积分的计算,会用到各种积分技巧,需要你充分发挥你的数学功底。

根据斯托克斯公式,这个曲面积分的答案,就等于你沿着那条闭合曲线做的曲线积分的结果!是不是很神奇?这感觉就像游戏里,你完成了任务,终获得了通关奖励。
为了让大家更清楚地明白,我整理了一个总结了斯托克斯公式的步骤:
| 步骤 | 操作 | 游戏类比 |
|---|---|---|
| 1. 验证条件 | 检查曲线是否闭合,曲面是否以曲线为边界 | 查看任务条件是否满足 |
| 2. 计算旋度 | 计算曲面的旋度向量场 | 学习技能,提升能力 |
| 3. 进行曲面积分 | 对旋度进行曲面积分 | 收集资源,完成目标 |
| 4. 得到结果 | 曲面积分结果等于曲线积分结果 | 获得游戏奖励,通关 |
当然,这游戏里还有很多技巧和策略。比如,选择合适的坐标系,能大大简化计算过程。这就像游戏里,选择合适的路线,能更有效率地完成任务。有时候,你可以利用对称性,或者一些特殊的积分公式,来简化计算。这就像游戏里,利用一些技巧和bug,可以更快地通关。
不同的题目,难度也不一样。有些题目很简单,几步就能算出来;有些题目就比较复杂,需要你动动脑筋,想一些巧妙的方法。这就像游戏里的不同关卡,有的简单,有的困难,需要你不断提升自己的技巧和策略。
我个人觉得,学习斯托克斯公式的过程,就像玩儿一个大型的解谜游戏。你需要掌握各种技巧,运用你的数学知识,一步步解开这个公式背后的秘密。这个过程虽然有些挑战,但终的成就感,是无法言喻的。
我玩儿这个“游戏”已经有一段时间了,从一开始的懵懵懂懂,到现在能够比较熟练地运用斯托克斯公式解决我感觉自己就像升级打怪一样,不断地提升自己的能力。
当然,这只是我个人的一点心得体会,我相信还有很多其他的技巧和方法,能够帮助大家更好地“玩儿”这个游戏。所以,大家可以一起交流一下,分享一下自己的经验和心得。你觉得在学习斯托克斯公式的过程中,还有什么技巧或方法?让我们一起探讨吧!