哎,斯托克斯公式这玩意儿,说简单也简单,说难也真够难的。感觉就像玩一个特别烧脑的游戏,一开始上手懵懵懂懂,玩儿久了,慢慢就找到感觉了。这篇文章就来聊聊我这个“游戏菜鸟”是怎么“攻略”斯托克斯公式的。
得承认,我刚开始接触这玩意儿的时候,完全一脸懵。各种向量、旋度、曲面积分……我感觉我的脑袋都要炸了。那些公式,密密麻麻的,看着就头大。这就像玩一个新游戏,刚开始看说明书,一堆术语,完全搞不懂是个啥。
不过,我这个人比较“佛系”,不喜欢死记硬背。我的“游戏攻略”就是:多练,多理解。我不会硬着头皮去啃那些复杂的公式推导,而是先从简单的例子入手,慢慢体会公式背后的含义。
就像玩游戏一样,先从新手村的任务开始做。我找了一些比较简单的例题,一步一步地跟着书上的解题步骤走。一开始,可能会卡壳,但没关系,慢慢来,多尝试几次,总能找到解题的思路。
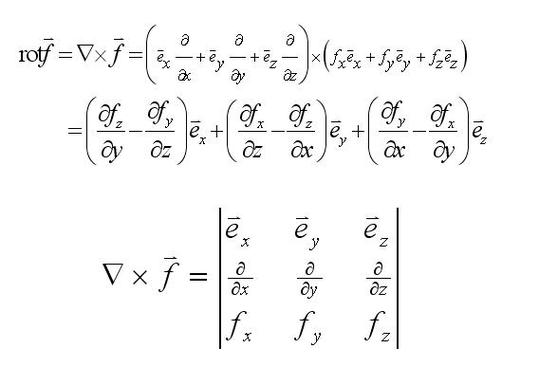
在这个过程中,我发现一个重要的技巧:画图!把题目的条件和已知信息都画出来,能更直观地理解题目。这就像玩一个策略游戏,把地图画出来,才能更好地规划自己的行动路线。
举个例子,计算一个封闭曲线的曲线积分。很多同学一看这题就懵了,积分上下限怎么定,积分路径怎么选?但如果我们把曲线画出来,再画出曲面,根据右手定则确定曲面的法向量方向,选择合适的坐标系,很多问题就迎刃而解了。
当然,光靠画图也不够,还得理解斯托克斯公式的本质。斯托克斯公式本质上是说,一个向量场的旋度在曲面上的积分等于该向量场在曲面边界上的环量。这就像玩一个RPG游戏,角色的属性值会影响游戏结果。斯托克斯公式中的旋度就像角色的属性,它决定了积分的结果。
为了更好地理解这个“游戏机制”,我特意整理了一个总结了斯托克斯公式的应用步骤:
| 步骤 | 操作 | 小技巧 |
|---|---|---|
| 1. 确定积分区域 | 明确曲线和曲面 | 画图!画图!画图! |
| 2. 计算旋度 | 根据公式计算向量场的旋度 | 注意偏导数的计算 |
| 3. 选择曲面 | 选择一个以曲线为边界的曲面 | 尽量选择计算简单的曲面 |
| 4. 计算曲面积分 | 计算旋度在曲面上的积分 | 选择合适的坐标系 |
| 5. 结果验证 | 检查结果是否合理 | 多做几道题,积累经验 |
在这个“游戏中”,我还发现了一些“隐藏彩蛋”。比如,斯托克斯公式可以简化一些复杂的曲线积分的计算。有些曲线积分,直接计算非常困难,但利用斯托克斯公式转化成曲面积分后,计算就变得简单多了。这就像玩游戏时,发现了一些隐藏的捷径,可以快速通关。
当然,这个“游戏”也不是一蹴而就的。在学习的过程中,我遇到过很多困难,也犯过很多错误。但正是这些错误,让我不断学习,不断进步。这就像玩游戏一样,失败是成功之母。只有不断地尝试,才能终掌握游戏的技巧。
学习斯托克斯公式就像一场马拉松,而不是百米冲刺。需要耐心,需要坚持,更需要理解。我建议大家不要害怕困难,一步一个脚印地学习,慢慢地就会掌握这个“游戏”的精髓。 多做练习,多思考,多你就能在这个“游戏中”玩得越来越溜。
我想问问大家,在学习斯托克斯公式的过程中,你们都遇到过哪些困难?又是如何克服的呢? 分享一下你们的经验,让我们一起“玩转”这个数学“游戏”吧!
