嘿,大家好!近我发现了一个挺有意思的东西,叫做维恩图,也有人叫它文氏图或者欧拉图。听起来很高大上是不是?其实没那么复杂,让我来用简单的语言跟你们唠唠嗑,保证让你一听就懂!
一开始,我看到“维恩图”这三个字,脑子里瞬间浮现出各种复杂的数学公式和抽象的图形,整个人都懵了。心想,这玩意儿肯定很难!结果,一查资料,才发现,其实它就是一种用图形来表示集合之间关系的工具。说白了,就是把一堆东西,用圈圈表示出来,然后看看这些圈圈之间是怎么重叠的。
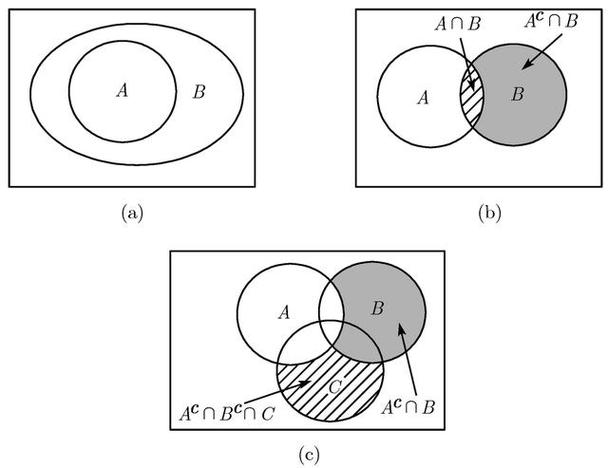
想象一下,你有很多喜欢的东西,比如:喜欢吃披萨,喜欢看电影,喜欢玩游戏。这三个爱好,你可以用三个圆圈来表示,每个圆圈代表一个爱好。如果这三个爱好有重合的部分,比如既喜欢吃披萨又喜欢看电影,那么这两个圆圈就会有重叠的部分。是不是很简单?
这就好比你参加一个同学聚会,有一些同学既喜欢打篮球又喜欢踢足球,还有一些同学只喜欢打篮球,还有一些同学只喜欢踢足球,甚至还有一些同学既不喜欢打篮球也不喜欢踢足球……那么,我们就可以用维恩图来表示这些同学之间的关系。用一个圆圈表示喜欢打篮球的同学,另一个圆圈表示喜欢踢足球的同学,重叠的部分就表示既喜欢打篮球又喜欢踢足球的同学。
当然,维恩图可不是只有两个圆圈那么简单哦!它可以有三个、四个,甚至更多个圆圈,表示更复杂的关系。 我初接触维恩图的时候,也觉得三个圆圈就够我头疼的了,更别提四个、五个了。不过,只要掌握了基本原理,其实也还好啦。
其实,维恩图的妙处就在于它直观易懂。它能把一些看起来很抽象的集合关系,用图形的方式清晰地展现出来,让大家一目了然。这对于那些不喜欢死记硬背数学公式的人来说,简直就是福音!
举个例子,我们来看一下两个集合的并集、交集和补集是如何用维恩图表示的。
| 集合运算 | 描述 | 维恩图示意图 |
|---|---|---|
| 并集 (A∪B) | 属于集合A或属于集合B的元素组成的集合 | 两个圆圈的并集区域(包括重叠部分) |
| 交集 (A∩B) | 同时属于集合A和集合B的元素组成的集合 | 两个圆圈重叠的部分 |
| 补集 (Ac) | 不属于集合A的元素组成的集合 (通常相对于一个全集而言) | 全集区域减去集合A的区域 |
是不是很直观?看到图,你就能立刻理解这些集合运算到底是什么意思了。这比一堆枯燥的公式要简单明了得多,对吧?
而且,维恩图的应用范围非常广泛。它不仅在数学中广泛使用,在逻辑学、计算机科学、概率论等等领域,也都能见到它的身影。甚至在日常生活中,我们也可以用维恩图来解决一些比如分析市场调查数据,或者规划自己的时间等等。
说到这里,我突然想起,以前学习概率论的时候,老师就用维恩图来解释事件的交集和并集。当时我还在纳闷,这玩意儿到底有啥用,现在想想,其实还挺方便的。它能很清晰地展示出不同事件之间的关系,让我们更容易理解概率的计算。
更有趣的是,我发现维恩图的历史还挺悠久的呢!它早是由英国数学家约翰·维恩在1880年左右发明的,在此之前,欧拉也曾经用类似的方法表示集合的关系。所以,有时候你也会听到“欧拉图”这个名字。不过,维恩对欧拉的方法进行了改进,使得维恩图更加完善和易用。
维恩图就是一个简单易懂、应用广泛的工具。它能帮助我们更好地理解集合之间的关系,解决各种如果你以前对它感到一头雾水,希望我的解释能让你豁然开朗。 如果你还有其他关于维恩图的或者有什么有趣的应用案例,欢迎留言分享哦! 让我们一起探索这个神奇的小工具吧!
